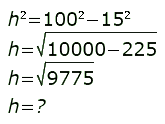Math
The Geometry of a Ktunaxa Fish Trap
Teacher Note: The Pythagorean Theorem will be discussed in this lesson and should not be used as an introduction to a unit on Pythagorean Theorem. Students will need a basic understanding of right triangles and the Pythagorean Theorem.
Learning Outcomes
The students will:
- Demonstrate an understanding of the Pythagorean relationship by calculating the measure of the third side of a right triangle, given the two other sides.
CONNECT
Goals:
The students will:
- Translate a 3-D shape into a 2-D shape drawing amenable to geometric calculations.
- Recognize and then calculate the height of a right triangle given the hypotenuse and the other two sides.
Task:
Students generate word problems using pictures, words, and symbols relating to a video example.
Activate Prior Knowledge:
- View drawings of Pacific Northwest Basket Traps.
- Watch the following video on the Ktunaxa Fish Trap.
Reminder: It is important to stop throughout the story and give students (A/B partners) opportunity to talk or respond to the story.
- Point out to students that the length of the sticks used in the fishtrap, including the sticks used to create the opening, were about the same. So, if overlap is included for the stick used to form the overlap, the length of each stick would be about 1 metre.
- Review the following information Pythagorean geometry:
- A right triangle has a 90 degree angle called a right angle.
- The side opposite the right angle is called the hypotenuse.
- The sides of a right triangle are often labelled a, b, and c, with c being the hypotenuse.
- The Pythagorean relationship of the sides in a right triangle states that a2 + b2 = c2
PROCESS
Predict and Question:
Given the previous information, ask the students what is the approximate height of a fishtrap. Students discuss with A/B partners the different height possibilities.
Procedure:
Algebra can be used to rearrange the following relationship, for the times that the length of the hypotenuse is known and the length of one of the other sides is known.
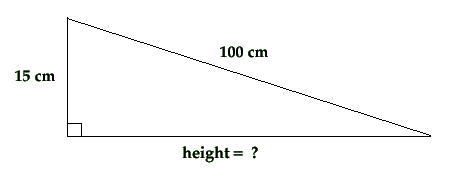
Information given for dimensions of a fishtrap:
- Radius = 15cm. This is one side of the triangle (a)
- Hypotenuse = 100cm. This side is (c)
Have the students draw and label a triangle to match the problem.
Using ‘h’ as the unknown, have students write a formula to match the problem.
h2 = 1002 – 152
Given the above formula, have the students solve the equation and then write a sentence to answer the problem. (Round to the nearest tenth of a centimeter)
TRANSFORM
Students generate word problems using pictures, words, and symbols relating to the video example. For example, a variety of word problems can be created by using the same formula as above and changing the data.
A/B Partners – Student partner groups trade their word problems with other partner groups and solve problems.
REFLECT
When can you use the formula a2 + b2 = c2 to solve a problem in real application? Use examples in your explanation.
Extend learning or next lesson
Students can find examples of right triangles and right triangle shaped objects in the local community to present to the class. The presentation can take many forms such as collages/videos/ photographs/drawings, etc. Students use the visual connection in order to apply the formula a2 + b2 = c2.